QML - Week 5

Regression models: the basics

Stefano Coretta

Word frequency and reaction times

What is the relationship between a word’s lexical frequency and reaction times in a lexical decision task in Croatian?

• Data from Lexical decision times for nouns from the Croatian Psycholinguistic Database.

• Lexical decision task (is it a real Croatian word?)

  • Reaction times.

  • Word frequency: counts from the Croatian web Corpus hrWaC.

Which relationship?

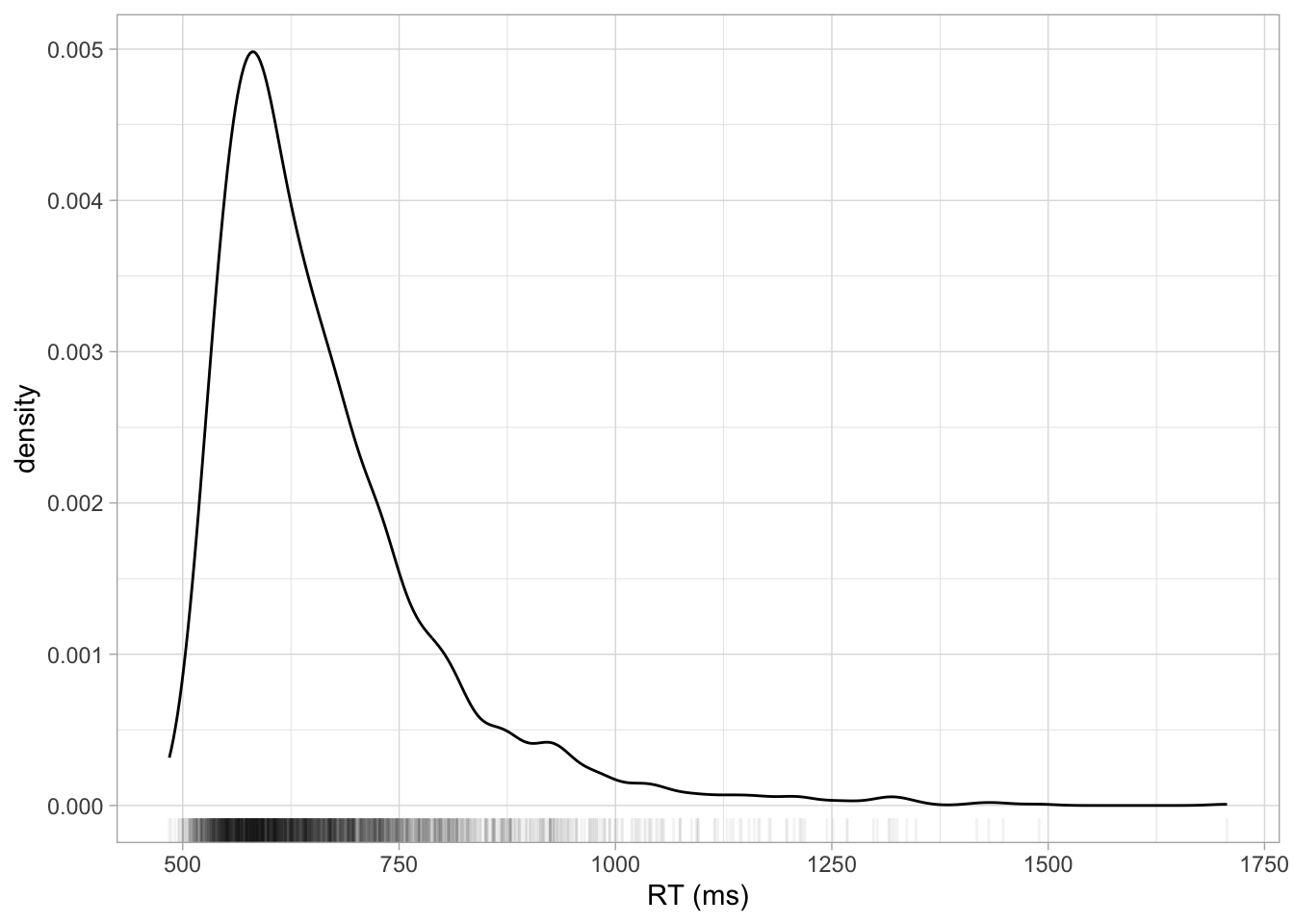
Reaction times

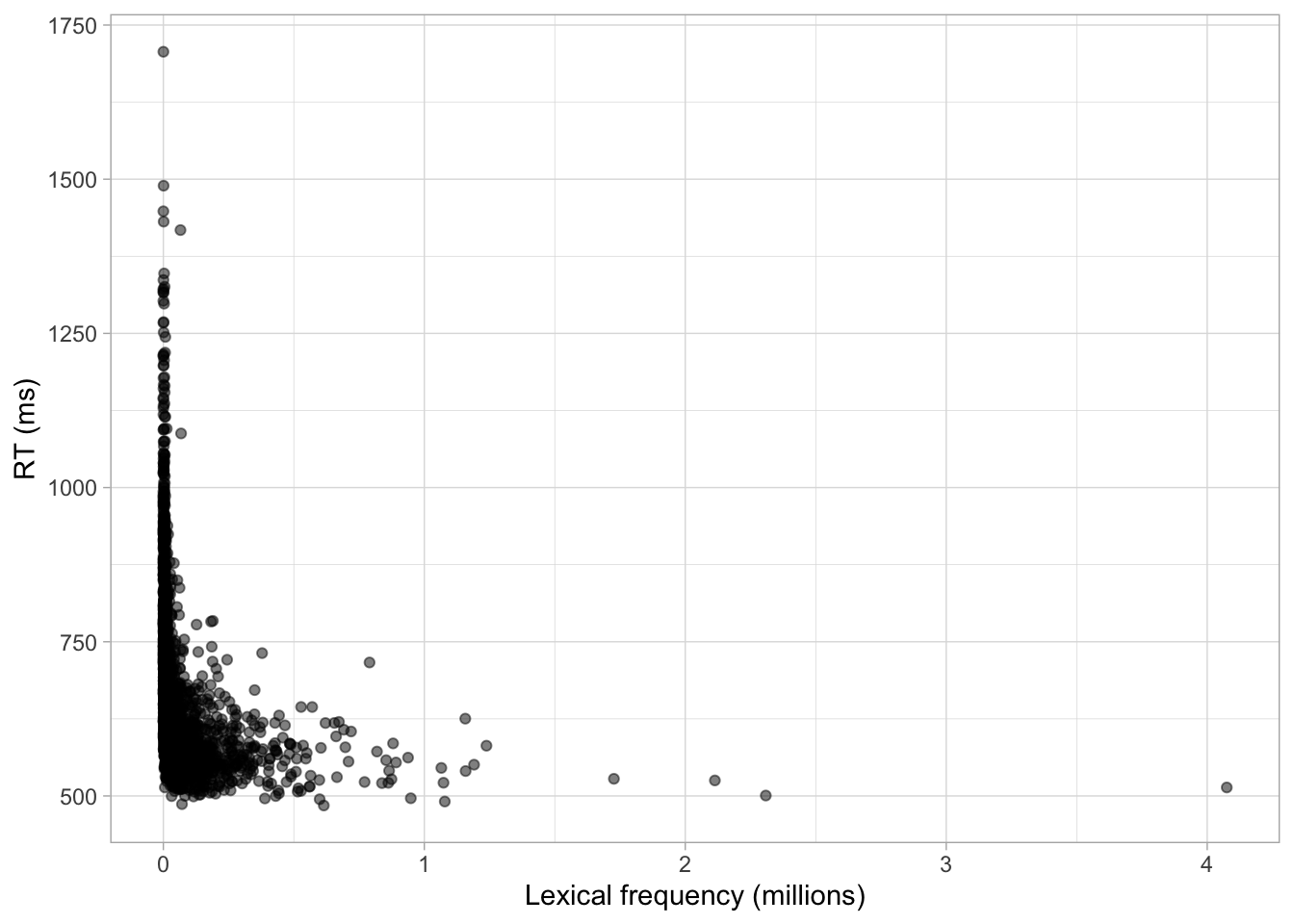
Word frequency and RTs

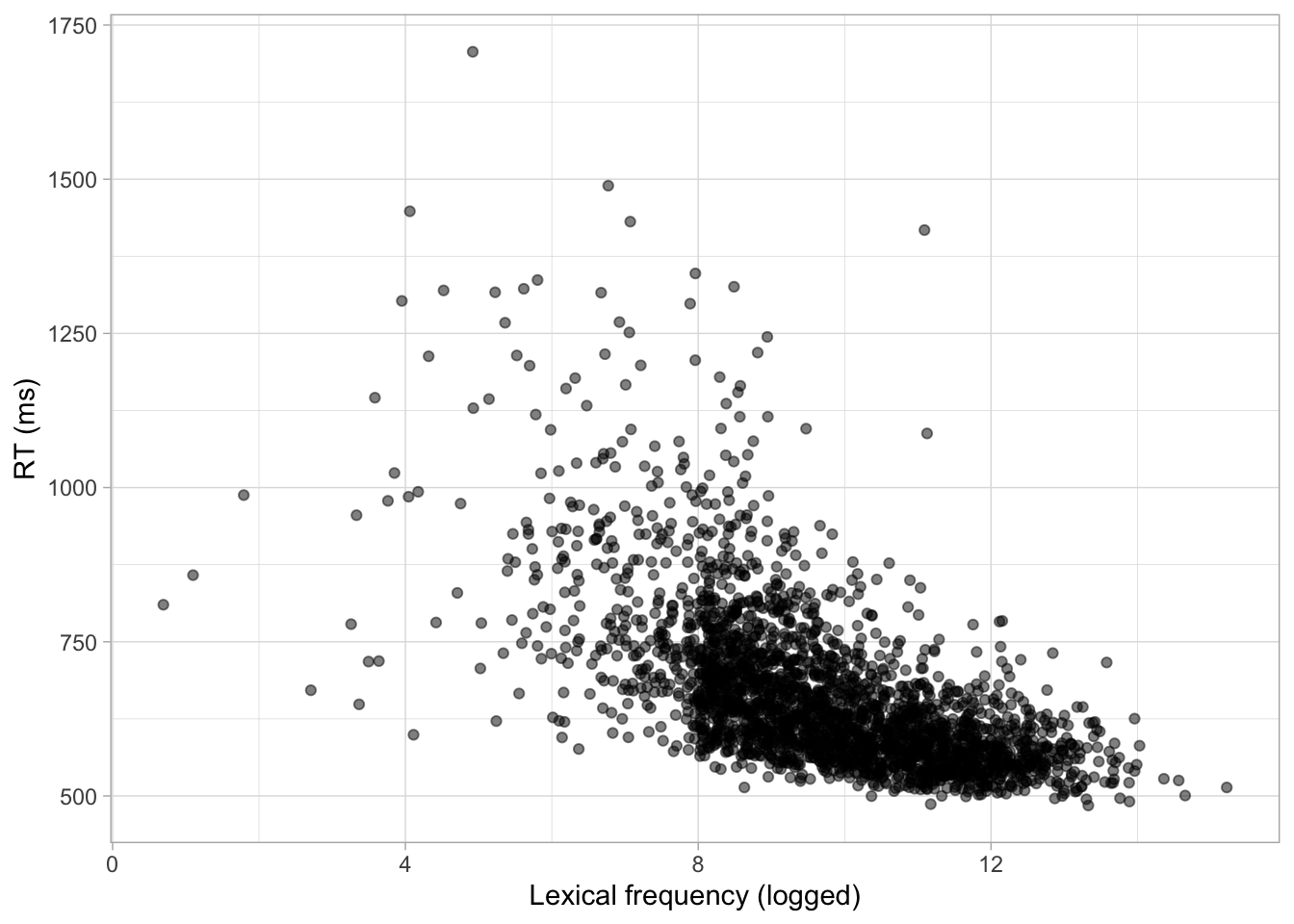
Logged word frequency and RTs

Gaussian model of RT

\[ RT \sim Gaussian(\mu, \sigma) \]

But we want to know what happens to RTs depending on the value of lexical frequency…

Then we let the mean \(\mu\) vary by lexical frequency!

\[ \begin{align} RT & \sim Gaussian(\mu, \sigma)\\ \mu & = \beta_0 + \beta_1 \cdot logf \end{align} \]

But what are those \(\beta_0\) and \(\beta_1\)?

The equation of a line

\[ y = \beta_0 + \beta_1 \cdot x \]

• Go to Linear models illustrated.

• \(\beta_0\) is the line intercept: the \(y\) value when \(x\) is 0 zero.

• \(\beta_1\) is the line slope: the change in \(y\) for each unit-increase of \(x\).

Regression model

\[ \begin{align} RT & \sim Gaussian(\mu, \sigma)\\ \mu & = \beta_0 + \beta_1 \cdot logf & \text{[Regression equation]} \end{align} \]

• A regression model is a model based on the equation of a line.

• The model estimates \(\beta_0\) (the intercept) and \(\beta_1\) (the slope) from the data (i.e. the observed \(RT\) and \(logf\) values).

• \(\beta_0\), intercept

  • Mean RT value when logged frequency is 0 zero (i.e. when word frequency is 1; exp(0) = 1).

• \(\beta_1\), slope

  • Change in mean RT for each unit increase of log-frequency (when log-frequency goes from \(x\) to \(x + 1\)).

Model’s posterior predictions

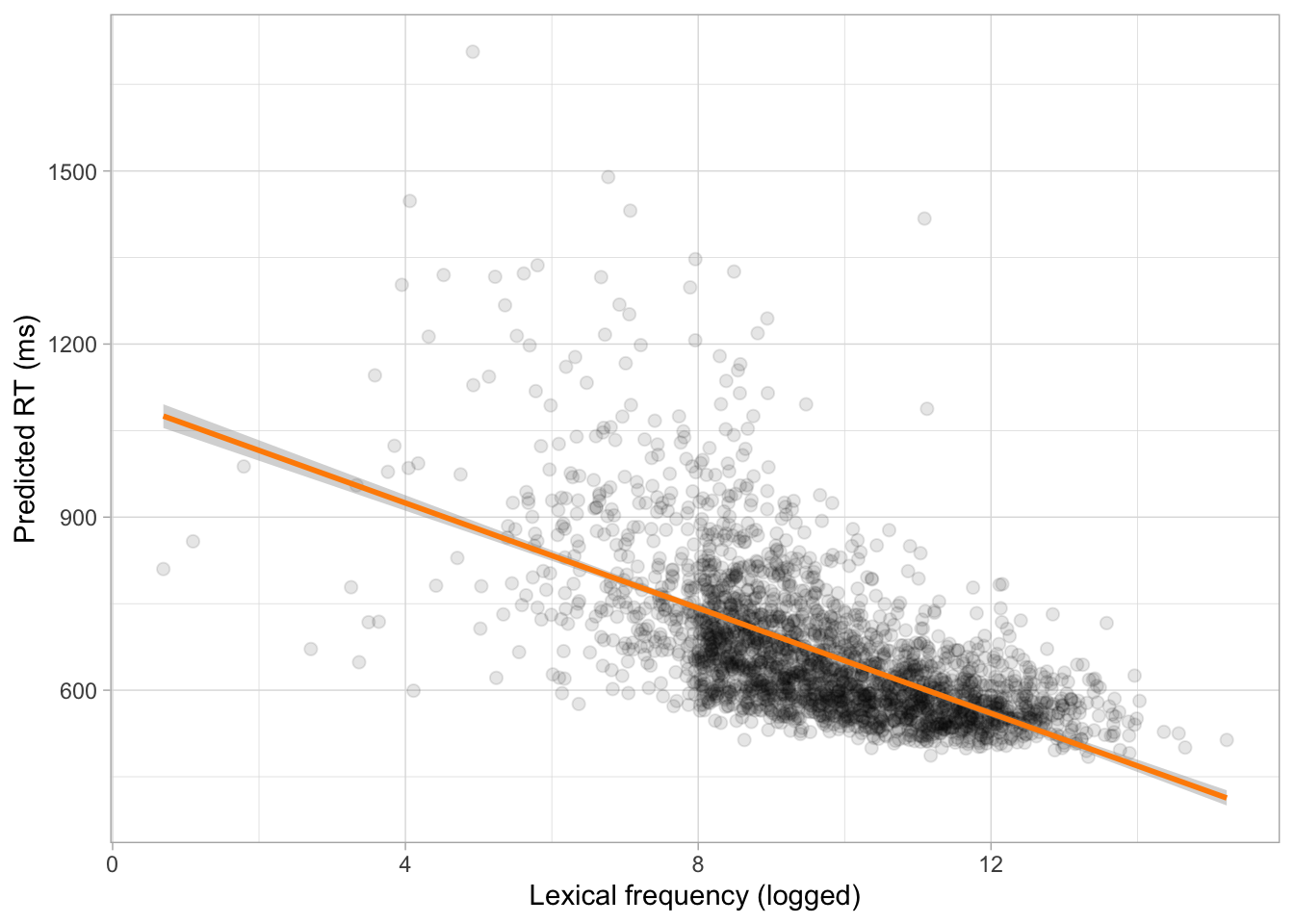
Word frequency and reaction times (bis)

What is the relationship between a word’s lexical frequency and reaction times in a lexical decision task in Croatian?

• When log-frequency is 0, the mean RTs are between 1084 and 1129 ms at 95% confidence.

• For each unit increase of log-frequency, the mean RTs decrease by 43-48 ms, at 95% confidence.

Correlation in NOT causation

Be careful!

• Correlation between two variables: they co-vary, i.e. they show a systematic association (their values tend to vary together in a consistent pattern).

• Spurious correlations: two variables can look correlated because of bias from another variable.

1. Number of plant names in a language vs. biodiversity of the region
   • Languages in biodiverse regions have more words for plants.
   • Mediator: cultural reliance on plants.
2. Language endangerment vs. economic development
   • Higher economic development is associated with greater language endangerment.
   • Confounder: colonial history.
3. Language prestige vs government policy
   • High prestige languages and officially supported languages each attract learners.
   • Collider: If you only look at languages with many learners, prestige and policy might appear related even if they’re not causally connected.

But it is if you use causal inference…

Causal inference

• Correlation can be interpreted causally if you adopt a causal inference approach.

• Learn about it in McElreath’s textbook Statistical Rethinking. Also check STeW.