Inference and uncertainty
1 Inference process
Imbuing numbers with meaning (see this section) is a good characterisation of the inference process.
Here is how it works. We have a question about something. Let’s imagine that this something is the population of British Sign Language signers.
We want to know whether the cultural background of the BSL signers is linked to different pragmatic uses of the sign for BROTHER.
But we can’t survey the entire population of BSL signers.1
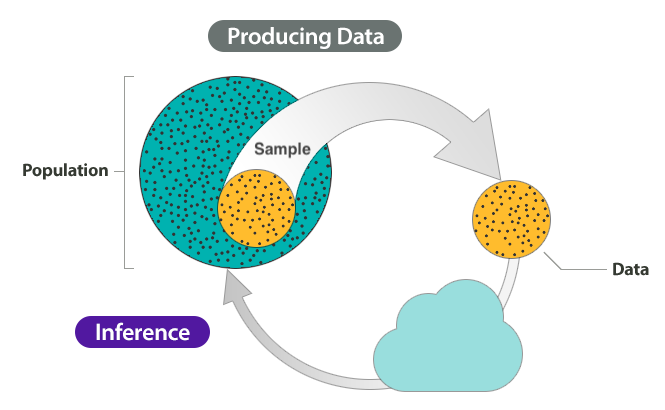
So instead of surveying all BSL users, we take a sample from the BSL population.
The sample is our empirical data (the product of our study or observation).
Now, how do we go from data/observation to answering our question about the use of BROTHER? We can use the inference process!
The figure below is a schematic representation of the inference process.
2 Inference is not infallible
However, inference, despite being based on data, does not guarantee that the answers to our questions are right or even that they are true.
In fact, any observation we make comes with a certain degree of uncertainty and variability.
3 Uncertainty and variability

Pliny the Elder was a Roman philosopher who died in the Vesuvius eruption in 79 CE. The only second certain thing must have been death.
Moving away from dark irony, as researchers we have to deal with:
Uncertainty in any observation of a phenomenon due to measurement error or because we can directly measure what we want to measure.
Variability among different observations of the same phenomenon due to natural and inevitable variability and measurement error.
The following picture is a reconstruction of what Galileo Galilei saw when he pointed one of his first telescopes towards Saturn, based on his 1610 sketch: a blurry circle flanked by two smaller blurry circles.

Only six years later, telescopes were much better and Galileo could correctly identify that the flaking circles were not spheres orbiting around Saturn, but rings.
The moral of the story is that at any point in history we are like Galileo in at least some of our research: we might be close to understanding something but not quite there yet.
4 Statistics as a tool
So what do we do with such uncertainty and variability? We can use statistics to quantify them!
Statistics is a tool that helps us quantifying uncertainty and controlling for variability.
But what is exactly statistics? Check What is statistics? to find out.
Footnotes
NOTE: Population can be a set of anything, not just a specific group of people. For example, the words in a dictionary can be a “population”; or the antipassive constructions of Austronesian languages…↩︎