Regression models: interactions between numeric predictors

Add and interpret interactions of two numeric predictors
Authors

Elizabeth Pankratz

Stefano Coretta

Published

October 2, 2024

Prerequisites

1 Introduction

Here you will learn how to include interactions between two numeric predictors and how to interpret the output. Relative to the other combination of predictor types, numeric-numeric interactions are more difficult to interpret: this is because a numeric predictor can take on many numeric values, and the numebr of combinations of values from two numeric predictors is even larger.

2 The data: Pankratz 2021

Let’s read the data.

library(tidyverse)

si <- read_csv("data/pankratz2021/si.csv")

The variables in this data frame that we’ll refer to in this tutorial are:

  • weak_adj: The weaker adjective on the tested scale (paired with the stronger adjective in strong_adj).
  • SI: Whether or not a participant made a scalar inference for the pair of adjectives in weak_adj and strong_adj (no_scalar if no, scalar if yes).
  • freq: How frequently the weak_adj co-occurred with a stronger adjective on the same scale in a large corpus.
  • semdist: A measure of the semantic distance between weak_adj and strong_adj. A negative score indicates that the words are semantically closer; a positive score indicates that the words are semantically more distant (the units are arbitrary).

Before we leap into modelling, though, let’s look in more detail at our predictors freq and semdist. A little bit of pre-processing is needed here, and the next sections will walk you through it.

2.0.1 Recoding SI

Now SI is coded with no_scalar for “participant did not make a scalar inference” and scalar for “participant made a scalar inference”.

Let’s convert SI into a factor with levels in the order c("no_scalar", "scalar") (note that this is the same order as the default alphabetical order, but it does not hurt to specify it ourselves).

si <- si %>%
  mutate(
    SI = factor(SI, levels = c("no_scalar", "scalar"))
  )

2.0.2 Transforming and centring freq

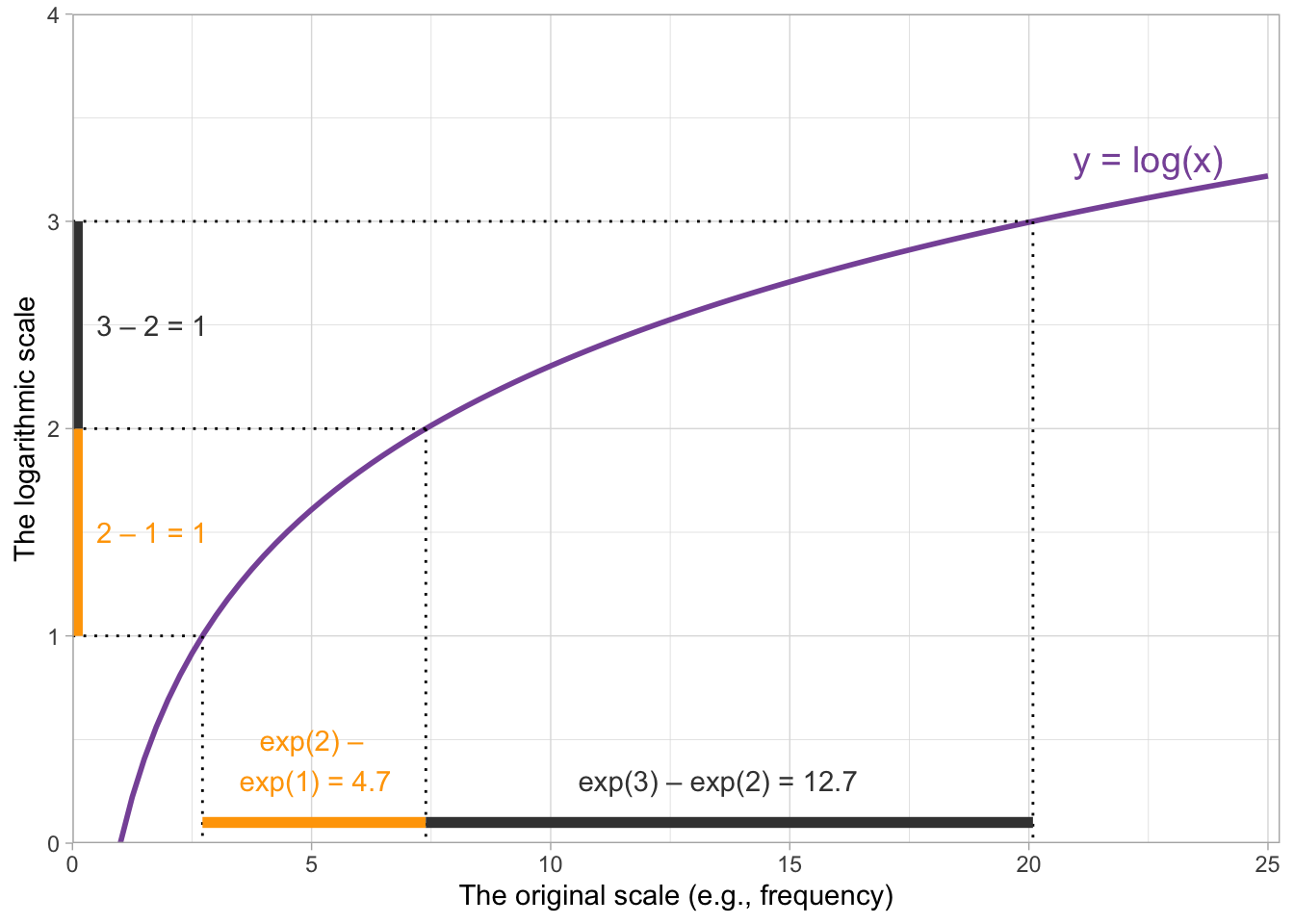
Frequencies notoriously yield an extremely skewed distribution, so it’s common practice in corpus linguistics to log-transform them before including them in an analysis.

Here’s how the frequencies look right out of the box:

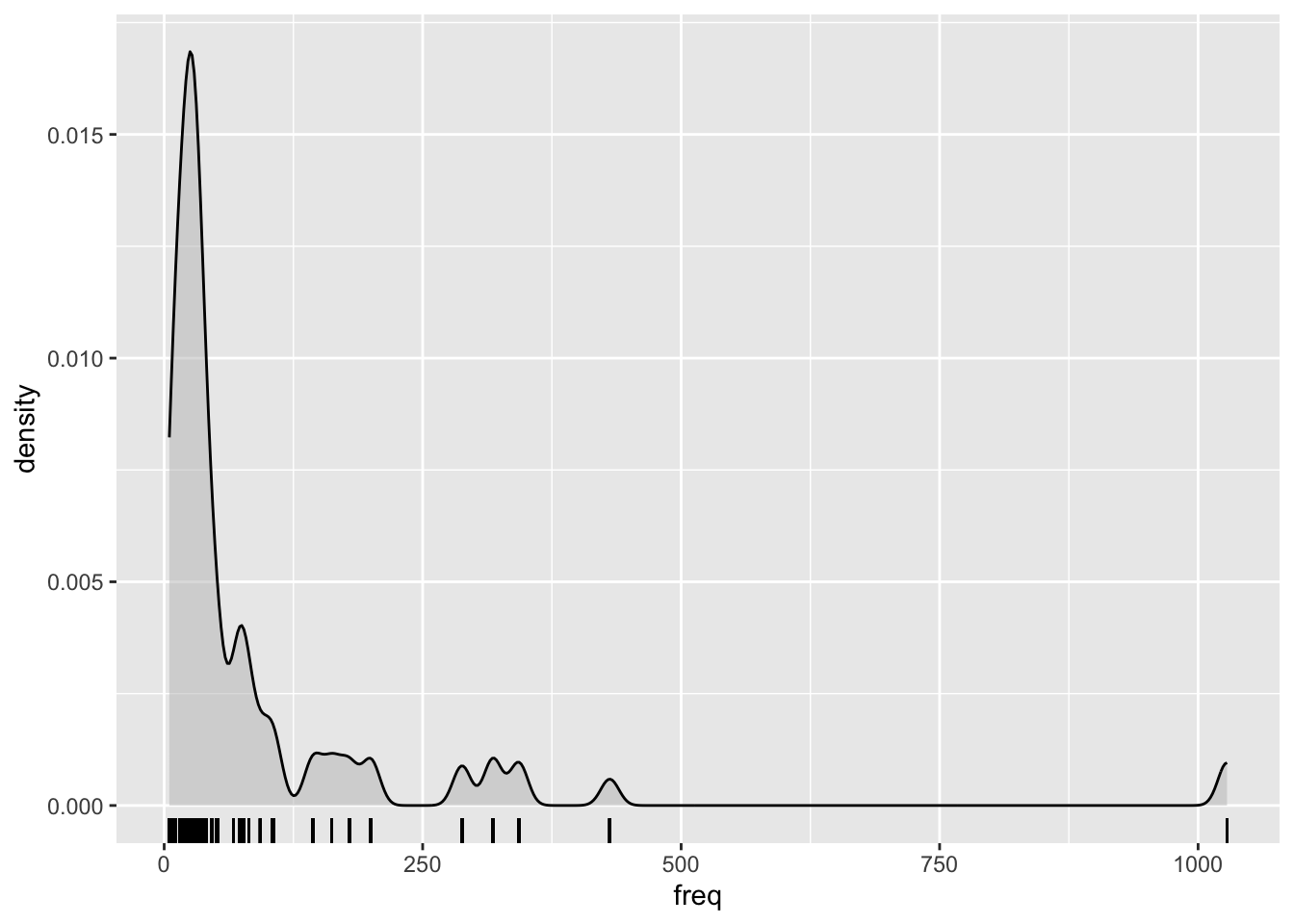
Log-transforming the frequencies helps to reduce the skewness. Use mutate() to take the log of freq and store the result in a new column called logfreq.

si <- si %>% 
  mutate(
    logfreq = log(freq)
  )

This is how the distribution of logged frequency looks like:

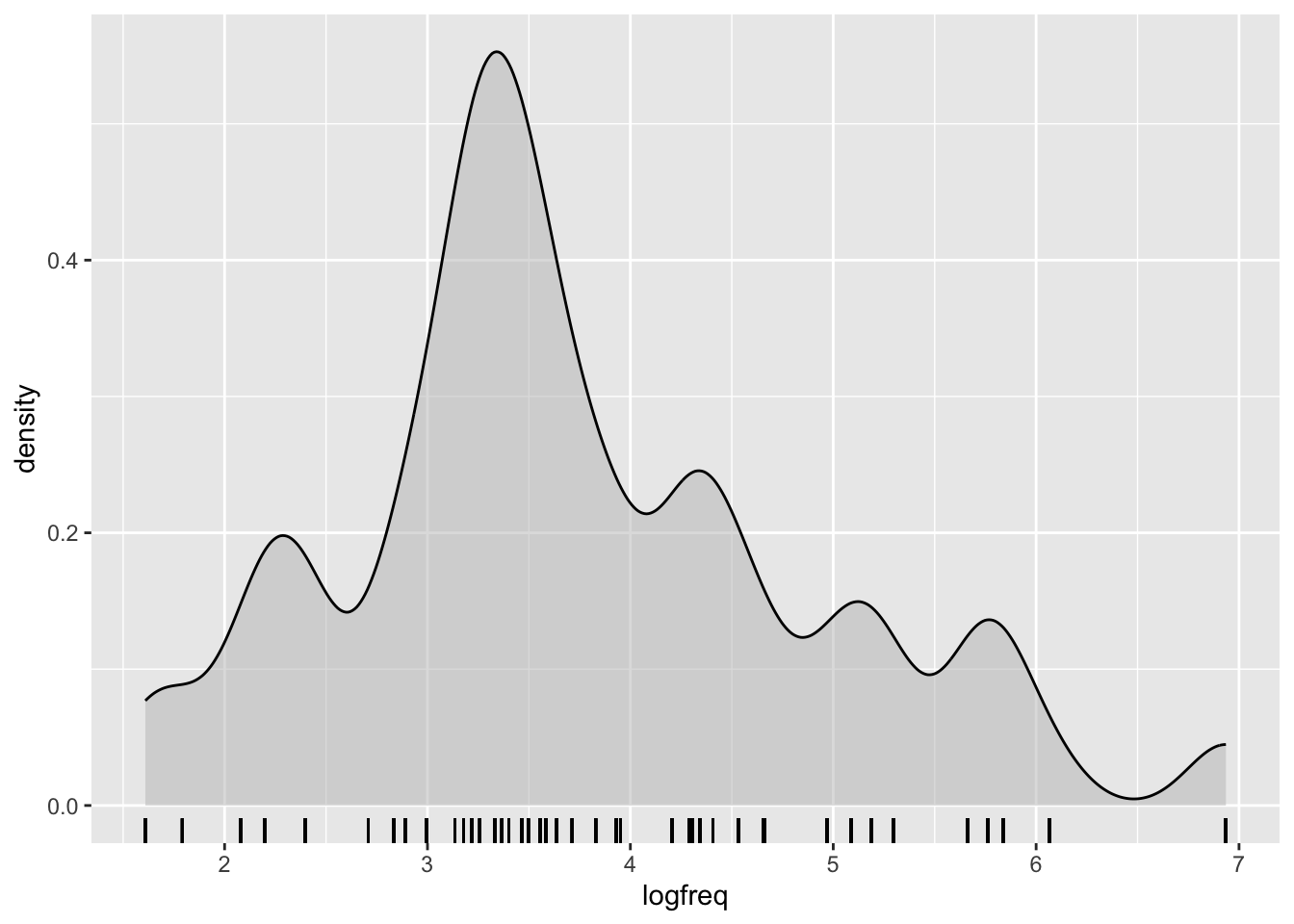
When we’re interpreting the model estimates below, we’ll be talking about the effect on scalar inferencing of one unit change on the log frequency scale. One unit change corresponds to moving from 0 to 1, from 1 to 2, 3 to 4, and so on…

When working with logged-transformed variables, you should keep in mind that a unit change on the logged scale does not corresponds to a unit change on the original scale.

Because the log transformation is non-linear, a unit change on the log frequency scale (e.g., going from 0 to 1, or going from 2 to 3) corresponds to different changes on the frequency scale, depending on which unit change on the log scale we evaluate.

To illustrate this:

The orange bars show that a unit change between 1 and 2 on the log scale corresponds to a change of 4.7 on the frequency scale, while the grey bars show that a unit change between 2 and 3 on the log scale corresponds to a change of 12.7 on the frequency scale.

We won’t be back-transforming log frequencies into plain old frequencies in this tutorial, but if you ever do, bear this in mind.

A good rule of thumb is to compute and report the change in the original scale that is associated with a unit change from the mean on the transformed scale to one unit above or below the mean.

We’re nearly done with logfreq—all that’s left is to centre it. To centre a variable, we compute its mean and subtract that from every observation of the variable. The goal is to get a new version of variable that has a mean of zero.

si <- si %>% 
  mutate(
    logfreq_c = logfreq - mean(logfreq)
  )

Don’t take our word! If you take the mean of the centred variable, it will be 0.

round(mean(si$logfreq_c))
[1] 0

The round() function is included because, for technical computational reasons, the mean actually comes out as an incredibly small number near 0, rather than 0 precisely. But in practice we can consider this incredibly small number near 0 to be 0. If you want to know why it is not precisely 0, see Floating Point Arithmetic.

logfreq_c is now ready to be used in our analyses. Next, you’ll take care of semantic distance on your own, and then we’ll move on to the modelling.

2.0.3 Centring semdist

Use mutate() to create a new, centred variable based on semdist that is called semdist_c. Verify that the mean of semdist_c is 0, and display semdist_c using a density plot with a rug, as above.

3 Visualise the data

Check Advanced plotting for a tutorial on how to plot the data.

4 Fitting the model

Here’s the mathematical specification of the model we’ll fit:

\[ \begin{aligned} \text{SI} & \sim Bernoulli(p) \\ logit(p) & = \beta_0 + (\beta_1 \cdot logfreq\_c) + (\beta_2 \cdot semdist\_c) + (\beta_3 \cdot logfreq\_c \cdot semdist\_c)\\ \end{aligned} \]

Write brm() code for this model, and name the variable you assign the model output to as si_bm.

  • The model formula should specify that we are predicting SI as a function of logfreq_c, semdist_c, and their interaction.
  • Use the appropriate model family.
  • The data comes from si.
  • Specify a seed for reproducibility.
  • Specify a file path to save the model fit to a file.1
si_bm <- brm(
  ...
)

Your model summary should look similar to this one.

summary(si_bm)
 Family: bernoulli 
  Links: mu = logit 
Formula: SI ~ logfreq_c + semdist_c + logfreq_c:semdist_c 
   Data: si (Number of observations: 2006) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
                    Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept              -0.70      0.05    -0.80    -0.59 1.00     3622     2389
logfreq_c               0.52      0.05     0.43     0.62 1.00     3291     2983
semdist_c               0.08      0.01     0.06     0.11 1.00     4171     2722
logfreq_c:semdist_c     0.05      0.01     0.03     0.07 1.00     3891     3009

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

4.1 Interpreting the estimates

Before we move to interpreting the estimate of this model, let’s just clarify something about numeric predictors and centred numeric predictors.

When a predictor is categorical and any contrast coding is used, the intercept of the model indicates the mean outcome value at the reference level of that predictor, and the other coefficients estimate the difference in mean outcome value between the other levels of the predictor and the value at the reference. If using indexing, rather than contrast coding, as we are in this course, then you get a coefficient for each level of the categorical predictor which is the estimate of the mean for that level.

With numeric predictors, the intercept indicates the mean outcome value when the numeric predictor is at 0.

The numeric predictor gets one coefficient estimate: this is the change in the outcome value when the numeric predictor goes from 0 to 1 (referred to as a unit change).

Note that the same estimate applies when going from 1 to 2, 2 to 3, 4.5 to 5.5 and so on. In other words, the change in the outcome value applies across any unit change of the numeric predictor.

Numeric predictors

The estimated coefficient of a numeric predictor corresponds to the change in the outcome value for each unit change in the predictor.

Now, when a continuous predictor is centred, 0 corresponds to whatever value is the mean of the non-centred predictor (1 in the centred predictor corresponds to the non-centred predictor mean + 1 unit, -3 corresponds to the mean - 3 units, whatever the units of the non-centred predictor are, and so on).

This means that the intercept of a model with centred numeric predictors corresponds to the outcome value when the numeric predictors are at their mean.

Now, let’s interpret the model estimates.

  • Intercept, \(\beta_0\): When centred log frequency and centred semantic distance are 0, there is a 95% probability that the log-odds of a scalar inference being made lie between –0.80 and –0.59.
  • logfreq_c, \(\beta_1\): When centred semantic distance is 0, for a unit change in (centred) log frequency, the change in log-odds of making a scalar inference is between 0.42 and 0.63 at 95% probability.
  • semdist_c, \(\beta_2\): When centred log frequency is 0, for a unit change in (centred) semantic distance, the change in the log-odds of making a scalar inference is between 0.06 and 0.11, at 95% confidence.

Since semantic distance and log frequency are centred, 0 on the centred predictors corresponds to the mean of the non-centred versions of the predictors. So we can also say:

  • Intercept, \(\beta_0\): When log frequency and semantic distance are at their mean, there is a 95% probability that the log-odds of a scalar inference being made lie between –0.80 and –0.59.
  • logfreq_c, \(\beta_1\): When semantic distance is at its mean, for a unit change in log frequency, the change in log-odds of making a scalar inference is between 0.42 and 0.63 at 95% probability.
  • semdist_c, \(\beta_2\): When log frequency is at its mean, for a unit change in semantic distance, the change in the log-odds of making a scalar inference is between 0.06 and 0.11, at 95% confidence.

Note how now we say “log frequency” and “semantic distance”, instead of “centred log frequency” and “centred semantic distance”

It is customary, when reporting results with centred predictors, to use the “non-centred” version of the report (so you would write e.g. “when log frequency is at its mean” rather than “when centred log frequency is at 0”).

As for logfreq_c:semdist_c, \(\beta_3\): As usual, this coefficient has two interpretations.

Interpreting the interaction between two numeric predictors:

(1) A unit change in (centred) log frequency is associated with a positive adjustment to the effect of (centred) semantic distance between 0.03 and 0.08 log-odds, at 95% probability.

  • In other words: As centred log frequency increases, the effect of semantic distance on the probability of a scalar inference being made increases as well.

(2) A unit change in (centred) semantic distance is associated with a positive adjustment to the effect of (centred) log frequency between 0.03 and 0.08 log-odds at 95% confidence.

  • In other words: As semantic distance increases, the effect of log frequency on the probability of a scalar inference being made increases as well.

The next section will walk you through how you can calculate conditional posterior probabilities when the model contains continuous predictors.

4.2 Conditional posterior probabilities

In previous weeks, to compute conditional posterior probabilities for categorical predictors, we would take the model equation, substitute the \(\beta\) coefficients with the estimates of the model and then calculate the posterior probabilities by substituting the predictor variables with 0 or 1s depending on the level we wanted to predict for.

Back then, it was easy to know which values to set the predictors equal to. But what do we do now that we have a numeric predictor that can, in principle, take on any value?

Rather than looking at the full range of values that the numeric predictor can take on, in practice we still choose just a few representative values to set the predictor to.

A common practice is to use the mean of the predictor and then the value that corresponds to 1 standard deviation above the mean and 1 standard deviation below the mean.

If you wish you can try and work out how to do the calculations yourself using the draws, but luckily there is a function from the brms package that simplifies things.

The function is conditional_effects() (aptly named!). It takes the model as the first argument and then a string specifying the effects to plot, here "logfreq_c:semdist_c" for “logfreq_c, semdist_c and their interaction”.

conditional_effects(si_bm, effects = "logfreq_c:semdist_c")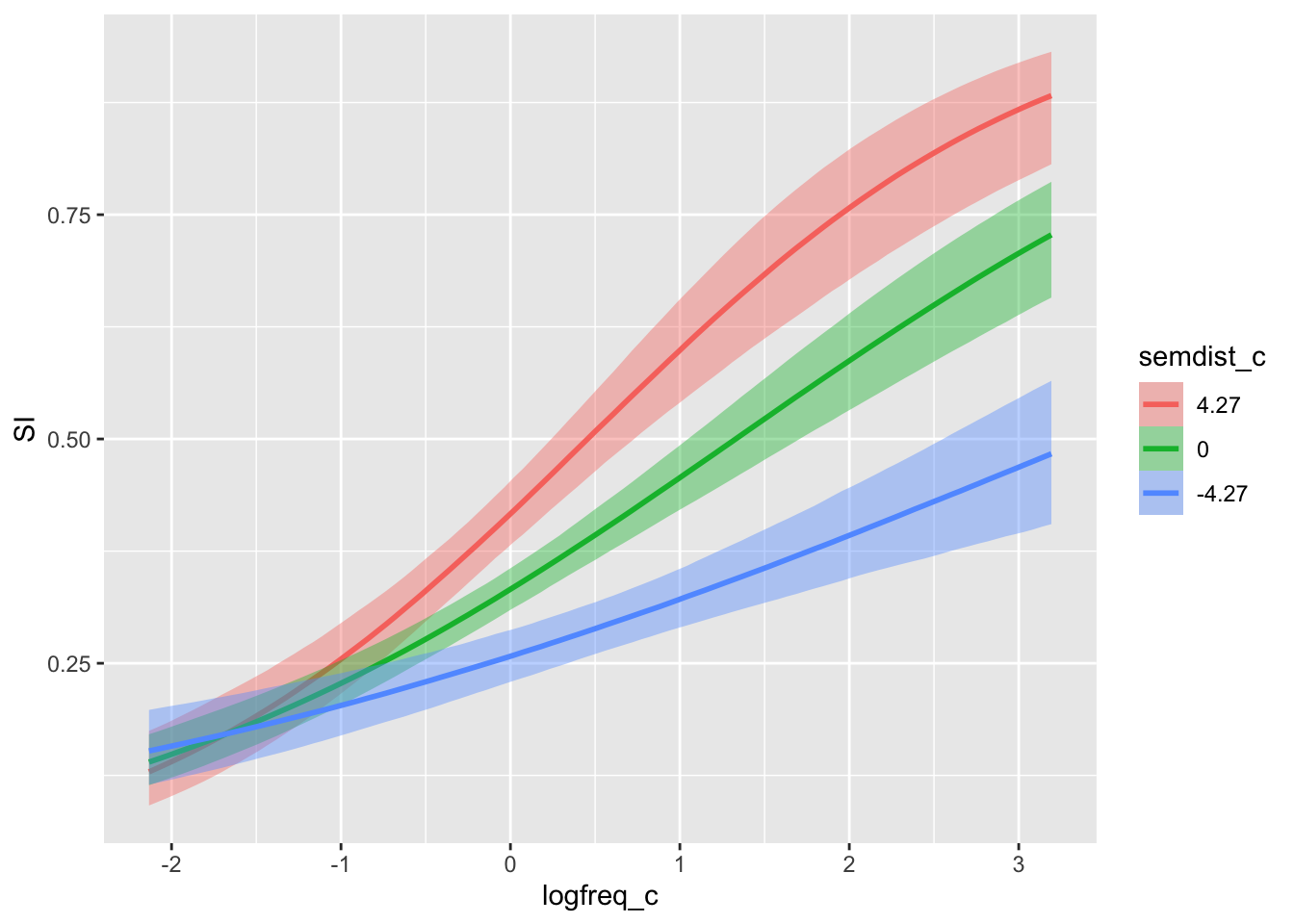

You will see that the plot has picked representative values for semdist_c (by default these are the mean, and mean \(\pm\) 1 standard deviation. You can calculate the mean and SD of semdist_c yourself to compare). Since we have listed logfreq_c first, the plot shows the entire range of values in logfreq_c.

The effect of log frequency gets stronger with increasing semantic distance.

We can invert the predictors to see the effect of semantic distance at representative values of log frequency.

conditional_effects(si_bm, effects = "semdist_c:logfreq_c")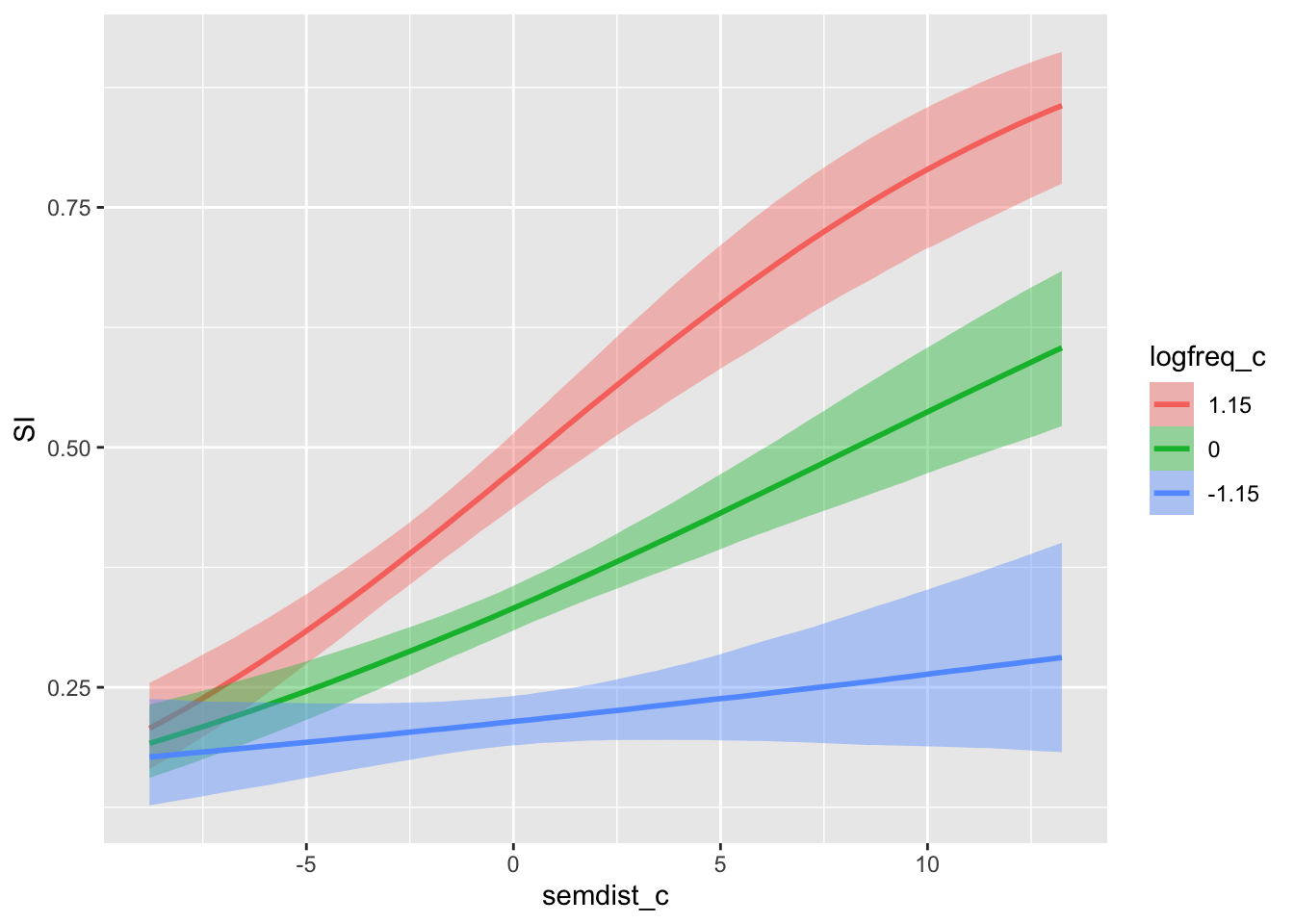

Here we see that, equivalently, the effect of semantic distance increases with increasing log frequency.

Prior to this week, we’ve been calculating and plotting posterior probabilities ourselves using the draws obtained with as_draws_df().

The conditional_effects() function is a great way of quickly plotting conditional posterior probabilities. If you feel like, go back to the models from previous weeks and try the function with those!

There is also a package, bayesplot, that has a lot of function that make plotting easier, so feel free to have a look at it if you wish.

Finally, tidybayes can also be helpful to work with draws and plotting and it’s worth looking.

5 Reporting

Now, let’s write a full report of model and results. Fill in the blanks yourself.

We fitted a Bayesian model to scalar inference (absent vs present), using a Bernoulli distribution. We included logged word frequency and semantic distance, and their interaction as predictors. Both predictors were centred.

The model’s results suggest that, when logged frequency and semantic distance are at their mean, the probability of a scalar inference being present is between … and …% (\(\beta\) = …, SD = …). For each unit increase of logged frequency, when semantic distance is at its mean, the probability increases by … to … log-odds (\(\beta\) = …, SD = …). For each unit increase of semantic distance, when logged frequency is at its mean, the probability increases by … to … log-odds (\(\beta\) = …, SD = …). The positive effect of logged word frequency increases with increasing semantic distance, by … to … log-odds (\(\beta\) = …, SD = …).

In the report we are just reporting log-odds for the continuous predictors. This is because the change in percent points depends on where on the continuous predictor scale you are calculating the change in percent points.

In real research contexts you would also report percent points at representative values of the continuous predictor (or values that are relevant for the research question).

Typical representative values are mean and mean \(\pm\) 1SD, as with the plots.

Things get much more complicated when working with the interaction term and generally percent points are not reported in that context.

Especially with Bernoulli models that include continuous predictors, the best way to understand and present the model results is by plotting them!

Footnotes

  1. The first time you run a model with this argument, that’s the version of the model that will be saved and loaded every time after. Beware of this if you use the same file argument to run a model that’s different from the final one you’ll want to run!↩︎